Rayon de courbure de la facette
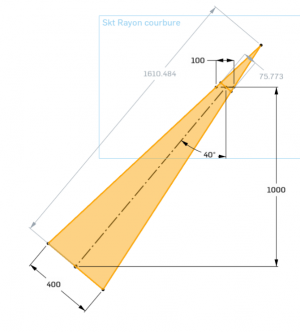
Afin d'obtenir un maximum de focalisation, les facettes du miroir de Fresnel peuvent être incurvées. Leur forme est optimisée pour la position dans laquelle :
- Soleil
- Récepteur
- Axe de rotation de la facette
sont alignés. Cette position correspond au cas ou la facette intercepte le plus de soleil.
Dans un premier temps, il faut déterminer la largeur visée (v=100mm sur le schéma), c'est à dire la largeur d'entrée du concentrateur secondaire (b) diminué, de part et d'autre, de la dispersion angulaire estimé. Pour les facettes contrale, la dispersion peut être prise au plus juste. Pour les facettes extrêmes, il faut parfois sous-évalué la dispersion pour assurer une plage de fonctionnement plus importante.
Pour le calcul de la distance focale (F), on peut utiliser le théorème de Thales. En effet, pour cette position, la facette de largeur f est perpendiculaire à l'alignement, et on peut facilement calculer la largueur projetée de la visée en multipliant par le cos(phi) (cela correspond à 75.773 sur le schéma) :
F/f = h/cos(phi) / (f -v . cos(phi))
D'ou
F = h/ (cos(phi)*(1-cos(phi) . v/f))
La facette peut être de forme parabolique avec un distance focal égale à F. Ou, plus simplement avec un rayon de courbure égale à deux fois la distance focale. Etant donné que la largeur de la facette est faible par rapport à la distance focal l'approximation est tout à fait acceptable. D'autant plus que, pour les autre position de la facette, on n'est pas dans l'axe optique.
Si on combine avec la dispersion angulaire, et que l'on appele b la largeur d'entrée du concentrateur secondaire :
Rc = 2.h / (cos(phi) * (1 - cos(phi) . (b - 2 . h . sin(delta) / cos(phi)² ) / f )
