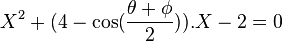Rayon de courbure de la facette
Afin d'obtenir un maximum de focalisation, les facettes du miroir de Fresnel peuvent être incurvées. Leur forme est optimisée pour la position dans laquelle :
- Soleil
- Récepteur
- Axe de rotation de la facette
sont alignés. Cette position correspond au cas ou la facette intercepte le plus de soleil.
La plage angulaire de focalisation de la facette est liée à la largeur d'entrée du concentrateur secondaire ç laquelle il faut ajouté l'élargissement du à la dispersion angulaire. Le rayon de coubure optimum provient découle d'un compromis entres ces trois caractéristiques. On peut en premier :
- Fixer la largeur visée
- Ou choisir la plage d'utilisdation
Mais, en général, il faut faire plusieurs itérations avant d'obtenir in comprimis acceptable
En fixant la largeur de visée
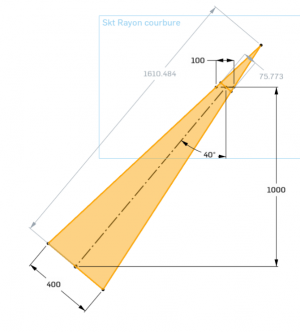
On commence par déterminer la largeur visée (v=100mm sur le schéma), c'est à dire la largeur d'entrée du concentrateur secondaire (b) diminué, de part et d'autre, de la dispersion angulaire estimée (c'est à dire "facilement" réalisable). Pour les facettes centrale, on peut, en générale prendre de la marge sur la dispersion. Pour les facettes extrêmes, il faut parfois sous-évalué la dispersion pour assurer une plage de fonctionnement plus importante.
Pour le calcul de la distance focale (F), on peut utiliser le théorème de Thales. En effet, pour la position d'alignement, la facette de largeur f est perpendiculaire à l'alignement, et on peut facilement calculer la largueur projetée de la visée en multipliant par le 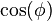 (cela correspond à 75.773 sur le schéma) :
(cela correspond à 75.773 sur le schéma) :
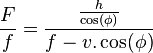
D'ou
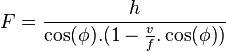
La facette peut être de forme parabolique avec un distance focal égale à F. Ou, plus simplement avec un rayon de courbure égale à deux fois la distance focale. Etant donné que la largeur de la facette est faible par rapport à la distance focal cette approximation est tout à fait acceptable, d'autant plus que, pour les autres positions de la facette, on n'est pas dans l'axe optique.
Si on combine avec la dispersion angulaire, et que l'on appelle b la largeur d'entrée du concentrateur secondaire :
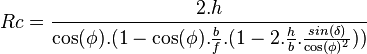
En fixant la plage d'utilisation
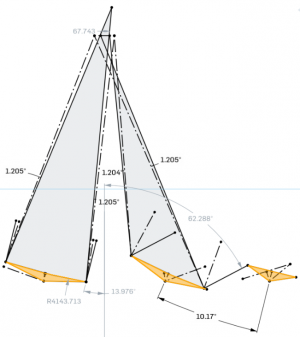
On fixe la plage d'utilisation, et on ajuste le rayon de courbure de façon que la tache ait la même largeur pour les deux configurations suivantes :
- alignement de la facette, du récepteur et du soleil
- angle d'incidence extréme de la plage d'utilisation sur la facette du même coté que le soleil
Comme les facettes font par paires symétriquees par rapport à l'axe du concentrateur, on peut représenté ces deux positions sur le même schéma en utilisant les deux facettes symétrique (voir schéma ci-contre).
A noter que l'ombre portée de la facette adjacente peut, en quelque sorte "réduire" la largeur de la facette et donc la tache réfléchie. Par exemple, sur le schéma, les taches réfléchies ne dépasse quasiment jamais la largueur de visée car l'ombre portée reduit sa largeur plus vite que sa défocalisation. Mais, pour bien faire, il faudrait aussi tenir compte du décalage entre les taches (sachant que chaque fcettes comporte une partie d'ombre portée).
En notant 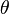 l'incidence extrême de la plage, on peut appliquer les formules précédente en remplaçant f par :
l'incidence extrême de la plage, on peut appliquer les formules précédente en remplaçant f par :
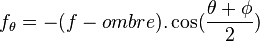
On obtient la position du foyer secondnaire. En premiére approche, on peut considérer que ce foyer secondaire est "symétrique du foyer principal. Ce qui permet, en l'absence d'ombre portée, on peut en déduire la largueur minimal de visée permettant in fonctionnement sur la plage d'incidence :
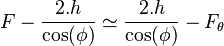
On pose : 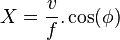
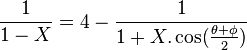
D'ou,, X est une solution de l'équation du second degré :