Trajectoire du Soleil : Différence entre versions
(→Hauteur h) |
(→Azimut a) |
||
| Ligne 28 : | Ligne 28 : | ||
L'azimut (angle entre le plan vertical passant par le soleil et le méridien du lieu) est donné par les équations: | L'azimut (angle entre le plan vertical passant par le soleil et le méridien du lieu) est donné par les équations: | ||
| − | sin(a)=cos( | + | <math>\sin(a) = \cos(\delta].\sin(\omega).\cos(h)</math> |
| − | |||
| − | Pour l'instant, ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme | + | <math>\cos(a)=-\cos(\Phi).sin(\delta) + \sin(\Phi).\cos(\delta).\cos(\omega).\cos(h)</math>\ |
| + | |||
| + | Pour l'instant, ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme équation du temps. | ||
| + | |||
| + | Une approximation de cette équation en fonction du jour d dans l'année est donnée par : | ||
| + | <math>\Delta T(d)=7{,}678\sin(B+1{,}374)-9,87\sin(2B)</math> | ||
| + | |||
| + | avec : <math>B(d) = \frac{2\pi(d-81)}{365}</math> | ||
=== Angles projetés === | === Angles projetés === | ||
Version du 11 février 2017 à 13:46
La trajectoire apparente du Soleil dans le ciel dépend à la fois de la période de l'année et du lieu de l'observation.
Sommaire
Définitions dans un repére géostationnaire
Les grandeurs utiles pour connaitre la trajectoire du Soleil sont les suivantes:
- Déclinaison δ
Angle entre les rayons du Soleil et le plan de l'équateur, période annuelle, positive en été (hémisphère nord), du 21 mars au 21 septembre. (−23,45°<δ<+23,45°)
- Angle horaire ω
Dû à la rotation de la Terre sur son axe, angle entre le méridien de l'observateur (longitude) et le méridien parallèle aux rayons du Soleil, période journalière (−180°<ω<+180°, midi solaire correspond à ω=0)
- Latitude géographique ϕ
Angle entre la verticale du lieu et le plan de l'équateur, positive dans l'hémisphère nord (−90°<ϕ<+90°)
Définitions pour l'observateur
Pour obtenir des grandeurs plus simples à visualiser, on définit la hauteur h et l'azimut a du Soleil. Ainsi, un observateur fixe en O, regardant au sud, doit pour viser le Soleil, tourner la tête d'un angle a puis lever la tête d'un angle h.
Hauteur h
La hauteur (angle du point visé avec le plan horizontal) est donnée par la formule :
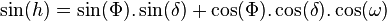
Azimut a
L'azimut (angle entre le plan vertical passant par le soleil et le méridien du lieu) est donné par les équations:
![\sin(a) = \cos(\delta].\sin(\omega).\cos(h)](/images/math/d/3/4/d3443037cdafaf54fffd1051c78e7f45.png)
 \
\
Pour l'instant, ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme équation du temps.
Une approximation de cette équation en fonction du jour d dans l'année est donnée par :
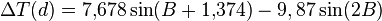
avec : 
Angles projetés
Dans le cas de la partir miroir de Fresnel du Concentrateur primaire, c'est la projection dans le repére lié au concentrateur qui à de l'importance (voir Définition des angles)
Ressources
Les justifications astronomiques des calculs de h et a peuvent être retrouvés par exemple dans la documentation en ligne de soleil-vapeur.org (première partie: Le capteur et la production de vapeur, Chapitre - Dossier de calculs).
Pour le lien temps solaire-temps légal, on peut aussi regarder ici: http://herve.silve.pagesperso-orange.fr/solaire.htm .
Nous avons développé des programmes Matlab permettant de calculer ces valeurs a et h en fonction de la date, de l'heure et de la position GPS. Ils peuvent être retrouvés sur le répertoire Github de osefrance.

