Repartition des facettes : Différence entre versions
| Ligne 9 : | Ligne 9 : | ||
Pour les facettes centrales, si on fixe phi (angle entre les position des facettes) et teta (l'angle d'apparition de l'ombre portée) : | Pour les facettes centrales, si on fixe phi (angle entre les position des facettes) et teta (l'angle d'apparition de l'ombre portée) : | ||
| − | beta = teta/2 - phi/4 | + | beta(1) = teta/2 - phi(1)/4 |
En projetant sur la normale au rayon incidents : | En projetant sur la normale au rayon incidents : | ||
| − | 2 h tan(phi/2) cos(teta) = (f / 2) (cos (beta) + cos(beta + phi)) | + | 2 h tan(phi(1)/2) cos(teta) = (f(1) / 2) (cos (beta(1)) + cos(beta(1) + phi(1)/2)) |
D'ou la formule qui permet de calculer la largeur maxi de la facette centrale : | D'ou la formule qui permet de calculer la largeur maxi de la facette centrale : | ||
| − | f = 4 h tan(phi/2) cos(teta) / (cos(beta) + cos(beta + phi/2)) | + | f(1) = 4 h tan(phi(1)/2) cos(teta) / (cos(beta(1)) + cos(beta(1) + phi(1)/2)) |
| + | |||
| + | Entre deux facette | ||
| + | |||
| + | beta(i) = beta(i-1) - phi(i)/2 | ||
| + | |||
| + | h (tan(phi(i)) - tan(phi(i-1))) cos(teta) = f(i)/2 * cos(beta(i)) + f(i-1)/2 * cos(beta(i) + phi(i)/2) | ||
| + | |||
| + | f(i) = 2 h (tan(phi(i)) - tan(phi(i-1))) cos(teta) / cos(beta(i)) - f(i-1) * cos(beta(i) + phi(i)/2) / cos(beta(i)) | ||
Version du 24 janvier 2017 à 19:09
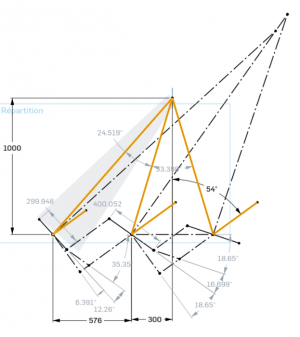
La répartition des facettes d'un miroir de Fresnel doit se faire de façon que l'ombre portée d'une facette sur la suivante apparaisse le plus taard possible. Pour cela il faut qu'elle apparaisse simultanément sur toutes les facettes du coté opposé à l'arrivé du soleil.
Sur le schéma, l'ombre portée apparaît pour environ 54° ala fois :
- Entre les deux facettes centrales
- Entre la facette centrale de gauche et la facette extérieure gauche lorsque le soleil vient de droite
Pour les facettes centrales, si on fixe phi (angle entre les position des facettes) et teta (l'angle d'apparition de l'ombre portée) :
beta(1) = teta/2 - phi(1)/4
En projetant sur la normale au rayon incidents :
2 h tan(phi(1)/2) cos(teta) = (f(1) / 2) (cos (beta(1)) + cos(beta(1) + phi(1)/2))
D'ou la formule qui permet de calculer la largeur maxi de la facette centrale :
f(1) = 4 h tan(phi(1)/2) cos(teta) / (cos(beta(1)) + cos(beta(1) + phi(1)/2))
Entre deux facette
beta(i) = beta(i-1) - phi(i)/2
h (tan(phi(i)) - tan(phi(i-1))) cos(teta) = f(i)/2 * cos(beta(i)) + f(i-1)/2 * cos(beta(i) + phi(i)/2)
f(i) = 2 h (tan(phi(i)) - tan(phi(i-1))) cos(teta) / cos(beta(i)) - f(i-1) * cos(beta(i) + phi(i)/2) / cos(beta(i))