Trajectoire du Soleil : Différence entre versions

Version actuelle en date du 11 février 2017 à 13:54

La trajectoire apparente du Soleil dans le ciel dépend à la fois de la période de l'année et du lieu de l'observation.

Sommaire

1 Définitions dans un repére géostationnaire
2 Définitions pour l'observateur
3 Ressources

Définitions dans un repére géostationnaire

Les grandeurs utiles pour connaitre la trajectoire du Soleil sont les suivantes:

Déclinaison δ

Angle entre les rayons du Soleil et le plan de l'équateur, période annuelle, positive en été (hémisphère nord), du 21 mars au 21 septembre. (−23,45°<δ<+23,45°)

Angle horaire ω

Dû à la rotation de la Terre sur son axe, angle entre le méridien de l'observateur (longitude) et le méridien parallèle aux rayons du Soleil, période journalière (−180°<ω<+180°, midi solaire correspond à ω=0)

Latitude géographique ϕ

Angle entre la verticale du lieu et le plan de l'équateur, positive dans l'hémisphère nord (−90°<ϕ<+90°)

Définitions pour l'observateur

Définition des angles, hauteur (h) et azimut (a) solaires.

Pour obtenir des grandeurs plus simples à visualiser, on définit la hauteur h et l'azimut a du Soleil. Ainsi, un observateur fixe en O, regardant au sud, doit pour viser le Soleil, tourner la tête d'un angle a puis lever la tête d'un angle h.

Hauteur h

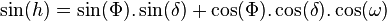
La hauteur (angle du point visé avec le plan horizontal) est donnée par la formule : $\sin(h)=\sin(\Phi).\sin(\delta) + \cos(\Phi).\cos(\delta).\cos(\omega)$

Azimut a

L'azimut (angle entre le plan vertical passant par le soleil et le méridien du lieu) est donné par les équations: $\sin(a) = \cos(\delta].\sin(\omega).\cos(h)$

$\cos(a)=-\cos(\Phi).sin(\delta) + \sin(\Phi).\cos(\delta).\cos(\omega).\cos(h)$ \

Angle solaire et equation du temps

Ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme équation du temps.

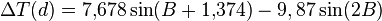
Une approximation de cette équation en fonction du jour d dans l'année est donnée par : $\Delta T(d)=7{,}678\sin(B+1{,}374)-9,87\sin(2B)$

avec : $B(d) = \frac{2\pi(d-81)}{365}$

et $\Delta T(d)$ exprimé en minute

Elle permet de corrigé $\omega$

$\omega_c = \omega + \Delta T(d) . \frac {2.\pi} {1440}$

Angles projetés

Dans le cas de la partir miroir de Fresnel du Concentrateur primaire, c'est la projection dans le repére lié au concentrateur qui à de l'importance (voir Définition des angles)

Ressources

Les justifications astronomiques des calculs de h et a peuvent être retrouvés par exemple dans la documentation en ligne de soleil-vapeur.org (première partie: Le capteur et la production de vapeur, Chapitre - Dossier de calculs).

Pour le lien temps solaire-temps légal, on peut aussi regarder ici: http://herve.silve.pagesperso-orange.fr/solaire.htm .

Nous avons développé des programmes Matlab permettant de calculer ces valeurs a et h en fonction de la date, de l'heure et de la position GPS. Ils peuvent être retrouvés sur le répertoire Github de osefrance.

@@ Ligne 16 : / Ligne 16 : @@
 == Définitions pour l'observateur  ==
-[[File;CS Position du soleil.png|frame|Définition des angles, hauteur (h) et azimut (a) solaires.]]
+[[File:CS Position du soleil.png|frame|Définition des angles, hauteur (h) et azimut (a) solaires.]]
 Pour obtenir des grandeurs plus simples à visualiser, on définit la hauteur h et l'azimut a du Soleil. Ainsi, un observateur fixe en O, regardant au sud, doit pour viser le Soleil, tourner la tête d'un angle a puis lever la tête d'un angle h.
@@ Ligne 22 : / Ligne 22 : @@
 === Hauteur h ===
-La hauteur (angle du point visé avec le plan horizontal) est donnée par la formule:
+La hauteur (angle du point visé avec le plan horizontal) est donnée par la formule :
-sin(h)=sin(ϕ)∗sin(δ)+cos(ϕ)∗cos(δ)∗cos(ω)
+<math>\sin(h)=\sin(\Phi).\sin(\delta) + \cos(\Phi).\cos(\delta).\cos(\omega) </math>
 === Azimut a ===
 L'azimut (angle entre le plan vertical passant par le soleil et le méridien du lieu) est donné par les équations:
-sin(a)=cos(δ)∗sin(ω)cos(h)
+<math>\sin(a) = \cos(\delta].\sin(\omega).\cos(h)</math>
-cos(a)=−cos(ϕ)∗sin(δ)+sin(ϕ)∗cos(δ)∗cos(ω)cos(h)
-Pour l'instant, ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme équateion du temps.
+<math>\cos(a)=-\cos(\Phi).sin(\delta) + \sin(\Phi).\cos(\delta).\cos(\omega).\cos(h)</math>\
+=== Angle solaire et equation du temps ===
+Ces valeurs sont données en fonction de l'angle solaire, c'est à dire du temps solaire vrai (indiqué par un cadran solaire). Le lien avec le temps solaire moyen ou légal (lu sur une montre) est complexe à cause de la trajectoire elliptique de la Terre. Ce lien est souvent désigné par le terme équation du temps.
+Une approximation de cette équation en fonction du jour d dans l'année est donnée par :
+<math>\Delta T(d)=7{,}678\sin(B+1{,}374)-9,87\sin(2B)</math>
+avec : <math>B(d) = \frac{2\pi(d-81)}{365}</math>
+et <math>\Delta T(d)</math> exprimé en minute
+Elle permet de corrigé <math>\omega</math>
+<math>\omega_c = \omega + \Delta T(d) . \frac {2.\pi} {1440}</math>
+=== Angles projetés ===
+Dans le cas de la partir [[miroir de Fresnel]] du [[Concentrateur primaire]], c'est la projection dans le repére lié au concentrateur qui à de l'importance (voir [[Définition des angles]])
 == Ressources ==