Définition des angles : Différence entre versions
(→Définition des angles de référence : Ajout de l'image) |
(→Définition des angles de référence) |
||
| Ligne 5 : | Ligne 5 : | ||
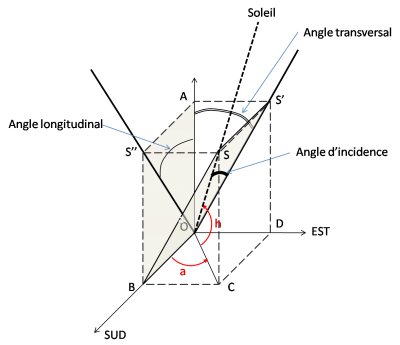
La position du Soleil dans le ciel est définie par les angles azimut (a) et hauteur (h) (angles en rouges, voir [[Trajectoire du Soleil]]). | La position du Soleil dans le ciel est définie par les angles azimut (a) et hauteur (h) (angles en rouges, voir [[Trajectoire du Soleil]]). | ||
On définit 3 angles pour caractériser la position du Soleil par rapport au concentrateur solaire: | On définit 3 angles pour caractériser la position du Soleil par rapport au concentrateur solaire: | ||
| − | * | + | * <math>\teta_l</math> : angle longitudinal, projection du rayon sur le plan (x,z). |
| − | angle longitudinal, projection du rayon sur le plan (x | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * <math>\teta_t</math> : angle transverse, projection du rayon sur le plan (y,z). | |
| − | + | * <math>\teta_i</math> : angle entre le rayon incident et le plan (y,z). | |
| − | Ces angles peuvent être exprimés en fonction de l'azimut et de la hauteur du Soleil. | + | <math>\teta_l</math> est utile pour orienter les miroirs du Fresnel afin qu'ils pointe vers l'absorbeur. |
| + | |||
| + | Dans le cas du démonstrateur, <math>\teta_i</math> est utiliser pour déterminer le décalage entre les miroirs primaires et l'absorbeur (inclinaison des rayons sur l'horizon). Dans le cas du prototype, cet angle permet de déterminer les pertes dues aux [[end loss]]. | ||
| + | |||
| + | Ces angles peuvent être exprimés en fonction de l'azimut et de la hauteur du Soleil. A noter que ces expressions varient selon l'orientation du concentrateur. | ||
== Orientation Nord-Sud == | == Orientation Nord-Sud == | ||
Version du 11 février 2017 à 14:01
Définition des angles de référence
La position du Soleil dans le ciel est définie par les angles azimut (a) et hauteur (h) (angles en rouges, voir Trajectoire du Soleil). On définit 3 angles pour caractériser la position du Soleil par rapport au concentrateur solaire:
- Échec d'analyse (fonction inconnue « \teta »): \teta_l : angle longitudinal, projection du rayon sur le plan (x,z).
- Échec d'analyse (fonction inconnue « \teta »): \teta_t : angle transverse, projection du rayon sur le plan (y,z).
- Échec d'analyse (fonction inconnue « \teta »): \teta_i : angle entre le rayon incident et le plan (y,z).
Échec d'analyse (fonction inconnue « \teta »): \teta_l est utile pour orienter les miroirs du Fresnel afin qu'ils pointe vers l'absorbeur.
Dans le cas du démonstrateur, Échec d'analyse (fonction inconnue « \teta »): \teta_i est utiliser pour déterminer le décalage entre les miroirs primaires et l'absorbeur (inclinaison des rayons sur l'horizon). Dans le cas du prototype, cet angle permet de déterminer les pertes dues aux end loss.
Ces angles peuvent être exprimés en fonction de l'azimut et de la hauteur du Soleil. A noter que ces expressions varient selon l'orientation du concentrateur.
Orientation Nord-Sud
tan(θl)=cos(a)/tan(h) tan(θt)=sin(atanh) sin(θi)=cos(a)∗cos(h)