Dispersion angulaire : Différence entre versions
(→Influence du rayon de courbure) |
(→Influence du rayon de courbure) |
||
| Ligne 45 : | Ligne 45 : | ||
== Influence du rayon de courbure == | == Influence du rayon de courbure == | ||
| − | + | [[File:CS RayonCourbure.png|thumbnail|Influence d'une erreur sur le rayon de courbure sur l'angle de réflexion.]] | |
| + | |||
| + | L'angle qui repère le centre de l'arc de cercle est donné par : | ||
tan(psi) = 2 R / f | tan(psi) = 2 R / f | ||
| Ligne 57 : | Ligne 59 : | ||
= f/2 (1+ (2R/f)²) | = f/2 (1+ (2R/f)²) | ||
| − | + | Pour un rayon de coubure de 2m et une facette de 400mm de largue, une erreur de +/-10% sur le rayon de courbure engendre une erreur d'angle d'environ 0.010 rad (environ 0.57°)de part et d'autre . | |
| − | + | Pour obtenir la déviation du rayon réfléchi, il faut multiplier cette valeur par 2. Soit une dispersion angulaire de prés de 1.2°. | |
Version du 29 janvier 2017 à 11:01
Lors d'une réflexion sur un miroir, il y a une certaine dispersion sur le rayon réfléchi. Dans le cas des facettes d'un miroir de Fresnel, cette dispersion a plusieurs causes :
- La dispersion sur le rayon incident (dans le cas d'un rayon solaire cela correspond au diamètre apparent du soleil : +/-0.27°)
- Les défauts de réflexion spéculaire fonction du matériau réflecteur utilisé
- Les défauts de fabrication (planéité ou circularité)
- L’erreur de réglage des facettes (et l'éventuelle divergence entre facettes)
- La précision du système de suivi du soleil
Pour caractériser la dispersion de façon précise, il faudrait définir la répartition de cette dispersion. A noter que selon l'origine de la dispersion, la répartition de la lumière réfléchie est différentes (gaussienne, linéaire, etc...). Mais pour la plupart des utilisations, on se contente de définir l'ensemble de ces dispersions par un simple angle de dispersion.
Dans le cas de la concentration solaire, pour une construction artisanale, on peut l'évaluer de +/-0.8° à +/-1.5°. Cet un paramètre important pour le dimensionnement d'un concentrateur solaire car il permet d'évaluer l'élargissement de la tache réfléchie et il permet de dimensionner le rayon de courbure des facettes et la largeur d'entrée du concentrateur secondaire.
| Dispersion (°) | Elargissement (mm) | Remarque |
| 0.27° | 4.7 | Taille apparente du soleil |
| 0.4° | 7.0 | |
| 0.6° | 10.5 | |
| 0.8° | 14.0 | Construction artisanale soigné avec tôle miroir |
| 1.0° | 17.5 | |
| 1.2° | 21.0 | |
| 1.5° | 26.2 | Facilement réalisable |
| 2.0° | 34.9 | Film réfléchissant "agro" |
Influence de l'angle
Dans le cas d'un miroir de Fresnel l'élargissement de la tache réfléchie est différent selon la position de la facette. En effet, par rapport à la facette centrale, les facettes extrêmes souffre de deux inconvénients :
- La distance facette-récepteur est plus grande
- L'angle d'arrivé sur le récepteur élargie la tache.
Au final, l'élargissement de la tache réfléchie par la facette positionnée par l'angle phi par rapport à la centrale est de 1/cos(phi)². Par exemple pour une facette positionné à 45°, élargissement est doublé.
Influence du rayon de courbure
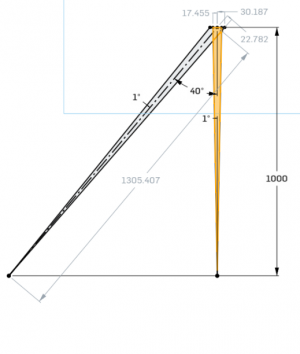
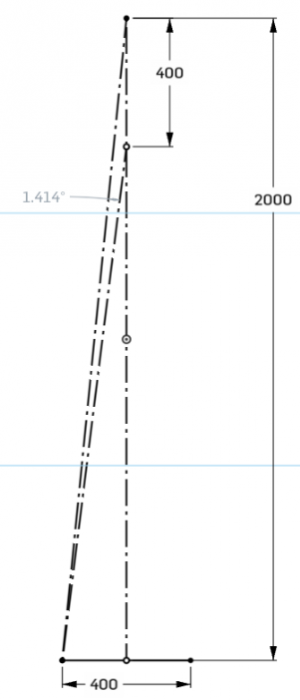
L'angle qui repère le centre de l'arc de cercle est donné par :
tan(psi) = 2 R / f
R = (f/2 ) tan(psi)
En dérivant :
dR/dphi = f/2 * d(tan (psi)) /dpsi
= f/2 (1+ (2R/f)²)
Pour un rayon de coubure de 2m et une facette de 400mm de largue, une erreur de +/-10% sur le rayon de courbure engendre une erreur d'angle d'environ 0.010 rad (environ 0.57°)de part et d'autre .
Pour obtenir la déviation du rayon réfléchi, il faut multiplier cette valeur par 2. Soit une dispersion angulaire de prés de 1.2°.